Copulas explained

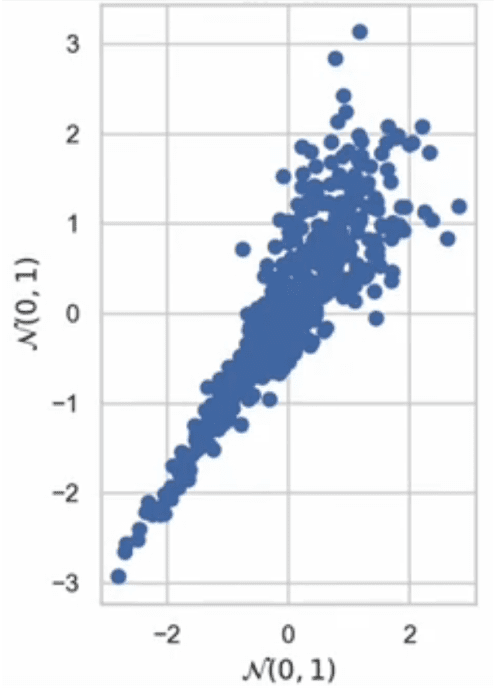
Let’s say you want to measure the relationship between multiple variables. One of the easiest ways to do this is with a linear regression (e.g., ordinary least squares). However, this methodology assumes that the relationship between all variables is linear. One could also use generalized linear models (GLM) in which variables are transformed, but again the relationship between the outcome and the transformed variable is–you guessed it–linear. What if you wanted to model the following relationship:

In this data, both variables are normally distributed with mean of 0 and standard deviation of 1. Additionally, the relationship is largely co-monotonic (i.e., as the x variable increases so does the y). However, the variables are vary closely correlated for small variables, but weakly correlated for large values.

Does this relationship actually exist in the real world? Certainly so. In financial markets, returns for two different stocks may be weakly positive related when stocks or going up; however, during a financial crash (e.g., COVID, dot-com bubble, mortgage crisis), all stocks go down and thus the correlation would be very strong. Thus, having the dependence of different variables vary by the values of a given variable is highly useful.

How could you model this type of dependence? A great series of videos by Kiran Karra explains how one can use copulas to estimate these more complex relationships. Largely, copulas are built using Sklar’s theorem.

Sklar’s theorem states that any multivariate joint distribution can be written in terms of univariate marginal distribution functions and a copula which describes the dependence structure between the variables.

https://en.wikipedia.org/wiki/Copula_(probability_theory)

Copulas are popular in high-dimensional statistical applications as they allow one to easily model and estimate the distribution of random vectors by estimating marginals and copulae separately.

Each variable of interest is transformed into a variable with uniform distribution ranging from 0 to 1. In the Karra videos, the variables of interest are x and y and the uniform distributions are u and v. With Sklar’s theorem, you can transform these uniform distributions into any distribution of interest using an inverse cumulative density function (that are the functions F-inverse and G-inverse respectively.

In essence, the 0 to 1 variables (u,v) serve to rank the values (i.e., percentiles). So if u=0.1, this gives the 10th percentile value; if u=0.25, this gives the 25th percentile value. What the inverse CDF functions do is say, if you say u=0.25, the inverse CDF function will give you the expected value for x at the 25th percentile. In short, while the math seems complicated, we’re really just able to use the marginal distributions based on 0,1 ranked values. More information on the math behind copulas is below.

The next question is, how do we estimate copulas with data? There are two key steps for doing this. First, one needs to determine which copula to use, and second one must find the parameter of the copula which best fits the data. Copulas in essence aim to find the underlying depends structure–where dependence is based on ranks–and the marginal distributions of the individual variables.

To do this, you first transform the variables of interest into ranks (basically, changing x,y into u,v in the example above). Below is a simple example where continuous variables are transformed into rank variables. To crease the u,v variables, one simply divides by the maximum rank + 1 to insure values are strictly between 0 and 1.

https://www.youtube.com/watch?v=KzgOncCdejw&list=PLJYjjnnccKYDppALiJlHskU8md904FXgd&index=8

Once we have the rank, we can estimate the relationship using Kendall’s Tau (aka Kendall’s rank correlation coefficient). Why would we want to use Kendall’s Tau rather than a regular correlation? The reason is, Kendall’s Tau measure the relationship between ranks. Thus, Kendall’s Tau is identical for the original and ranked data (or conversely, identical for any inverse CDF used for the marginals conditional on a relationship between u and v). Conversely, the Pearson correlation may vary between the original and ranked data.

Then one can pick a copulas form. Common copulas include the Gaussian, Clayton, Gumbel and Frank copulas.

The example above was for two variables but one strength of copulas is that can be used with multiple variables. Calculating joint probability distributions for a large number of variables is often complicated. Thus, one approach to getting to statistical inference with multiple variables is to use vine copulas. Vine copulas rely on chains (or vines) or conditional marginal distributions. In short, one estimat

For instance, in the 3 variable example below, one estimates the joint distributions of variable 1 and variable 3; the joint distirubtion of variable 2 and variable 3 and then one can estimate the distribution of variable 1 conditional on variable 3 with variable 2 conditional on variable 3. While this seems complex, in essence, we are doing a series of pairwise joint distributions rather than trying to estimate joint distributions based on 3 (or more) variables simultaneously.